В предыдущей главе мы пришли к выводу, что прибыль любой компании можно рассмотреть в виде математической модели или моделей.
Продемонстрируем данный подход на задаче СКВОЗНОГО ПРИМЕРА.
(!) На практике, чтобы сделать это, вы будете вынуждены "погружаться" в бизнес заказчика. И если вам потом никогда не пригодятся знания, "сколько раз доится корова и сколько литров она отдает в утренней и вечерней дойке в зависимости от разных параметров" (а это является частью "математикой прибыли" вашего заказчика), то примите это за издержки данного вида деятельности. Но, к сожалению, сложно сделать проект успешным, если вы не понимаете "уровень математики прибыли" - достаточно сложно.
Маловероятно, что то, что будет описано ниже пригодится вам когда-либо. Это и есть "издержки" профессии интегратора. Чтобы автоматизировать компанию-заказчика, вам нужно понять математику прибыли. Чтобы понять СКВОЗНОЙ ПРИМЕР - вы вынуждены тратить время на то, что вам может быть никогда больше не пригодится.
Как всегда все легче понять на примере. Для примера рассмотрим ставки на событие - "подброс монетки".
Вероятность "орел" или "решка" 50% на 50%. Представим, что мы принимаем ставки на "орла и решку". Коэффициент на победу мы установили равный двум. То есть если игрок "поставил" 1 рубль, в случае выигрыша - получил два рубля ("свой" и еще один). В случае проигрыша рубль остается в кассе.
А теперь представим, что у нас всегда играет два игрока, и оба ставят по одному рублю причем на разные стороны монетки. Один ставит на "орла", а второй "на решку". См. рисунок ниже.

В кассе после ставок оказывается два рубля. А после "поброса монетки" один из двух игроков выигрывает и мы вынуждены отдать ему два рубля (1 рубль умноженный на 2). И так раз за разом. См. рисунок ниже.

А теперь следующий шаг. Мы назначили коэффициент на победу равным не два (2), а полтора (1.5). Игроки продолжили ставить по одному (1) рублю, но теперь из двух (2) рублей в кассе нам приходится отдавать победителю не два (2) , а полтора (1.5) рубля. А пол (0.5) рубля остается нам. См. рисунок ниже.

Теперь каждый раз после розыгрыша события у нас остается пол (0.5) рубля. Как можно оценить прибыль для букмекера? В первом приближении это делается так: (см.рисунок ниже)
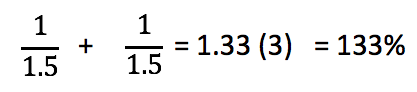
33% (133% - 100%) - коэффициент, который выражает прибыль букмекера.
(!) Правда это не рентабельность, а наценка. Тj есть, чтобы получить прибыль, нам нужно умножить на этот коэффициент не Выручку (2 рубля), а себестоимость (1.5 рубля). Но рентабельность считается сложнее, и для наших целей это - это излишняя сложность, поэтому мы опустим это.
При коэффициенте равном мы все возвращаем игрокам (100%-100%=0%)
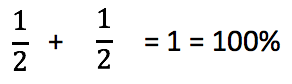
Нам осталось рассмотреть еще 2 ситуации и перейдем к практической части.
А что если один игрок поставил как всегда один (1) рубль, а второй - четыре (4) рубля? См. рисунок ниже.
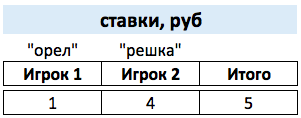
В этом случае букмекер включается в игру, то есть одном случае выиграет, а в другом случае проиграет деньги. См. рисунок ниже.
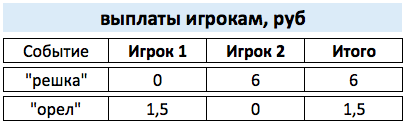
В случае, если выпадет "орел" в кассе останется 5 - 1,5 = 3,5 рубля. А в случае, если выпадет "решка" то в кассе будет 5 - 6 = - 1 рубль. То есть букмекер сам стал игроком.
Это допустить нельзя, так как возможно, что будут такие большие выплаты, что букмекер может банкротиться. Достаточно всего одного раза, чтобы игроки перестали доверять.
Букмекер поступает в таких случаях следующим образом... Либо он увеличит коэффициент на "орла" и уменьшит на "решку", чтобы ставками следующих игроков компенсировать этот перекос или даже сам делает ставку у других букмекеров на "орла" (и потеряет при этом маржу).
Рассмотрим последнюю ситуацию и перейдем к практической реализации.
Что будет, если события "орел-решка", не равновероятные? Например, одна сторона монетки такая тяжелая, что орел выпадает чаще, чем решка. Например 80% выпадает "орел" и всего 20% - "решка". Тогда ставки должны будут распределиться по-другому. Для простоты расчетов предположим, что мы согласны на прибыльность 0%. Тогда коэффициенты будут 1,25 (1/80%) и 5 (1/20%). Тогда для того, чтобы выигрыш одного игрока не повлек за собой убытки, то ставки должны быть... см. рисунок ниже.
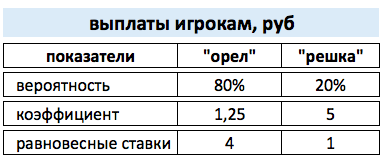
Равновесные ставки четыре (4) и один (1) рубль. Проверяется очень просто:
4 * 1,25 = 5 * 1
Формула для расчета будет очень простой:
Сумма ставок 1 * k1 = Сумма ставок 2 * k2
Если у нас событие состоит не из двух вариантов (как в монетке), а большего количества вариантов, как в скачках (где 8 вариантов, а не 2), то принципиально ничего не изменится, нам нужно, чтобы ставки были такими, чтобы соблюдалось равенство:
Сумма ставок 1 * k1 = Сумма ставок ... * k... = Сумма ставок 8 * k8
В этом случае суммы ставок и выплат выигрышей будут равны заложенной в коэффициенты маржой (или наценкой).
Теперь можно сказать, что прибыль зависит от величин ставок, маржи заложенной в коэффициенты и равномерностью распределения ставок.
(!) Причем сумма ставок зависит от того, какая маржа заложена в коэффициенты. Игроки считают маржу букмекера или чувствуют, когда коэффициенты слишком низкие, и просто игнорируют такие Забеги. Управление этими параметрами и являются и управление кого с кем поставить в Забег - и является ядром управления данного бизнеса.
Тогда можно рассмотреть как сформировалась прибыль за любой промежуток времени. См. рисунок ниже.
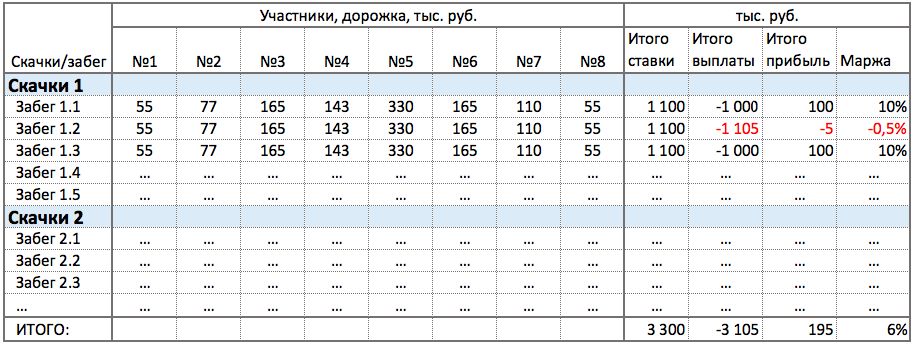
В отчете можно увидеть, как формировалась прибыль. Можно увидеть и абсолютные и относительные показатели, а также забеги, которые по каким-то причинам привели убыткам.
То есть по таким Забегам требуется дополнительный анализ. Например, на какое-то событие были не сбалансированы ставки. Возможно, нужен другой отчет. См. пример ниже.
В отчете видно, что не все ставки сбалансированы, и Забег 1.2 и попал на несбалансированную ставку. А Забег 1.3 тоже не сбалансирован, но свершилось другое событие.
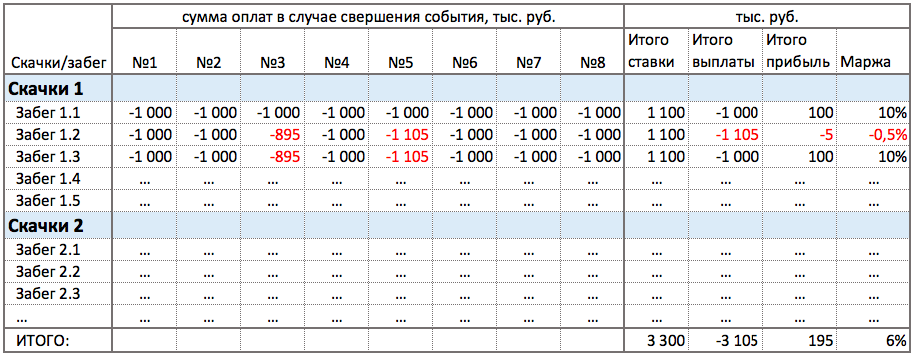
(!) СКВОЗНОЙ ПРИМЕР выбран условно, он не является описанием реального проекта. Возможно, что на практике отчеты выглядят как-то иначе. Но для целей главы и курса - это не важно.
Подведем итоги главы: Цель этой главы была не только в решении СКВОЗНОГО ПРИМЕРА, но и в том, что любую компанию и бизнес можно представить в виде математической модели и выразить ее в отчете или серии отчетов, которые позволят понять, как сформировалась прибыль и позитивный или негативный это сценарий по сравнению с другими периодами, Скачками и т.д. И нет компаний, для которых бы не возможно было сформировать схожую модель.
